1. Introduction
Global water scarcity is on the rise, and approximately two-thirds of the world’s population experience severe shortage at least once a year; by 2050, estimates say, nearly six billion people will suffer from clean-water scarcity.[1] The challenges are in both supply and demand: natural flows are reduced during dry months in many parts of the world, due to extensive supply-side engineering interventions that have fragmented river systems; pollution levels in water have increased due to anthropogenic activities, including industrial effluents and unsustainable agriculture; and rapid population and economic growth have increased the demand for water. Water use has grown at more than twice the rate of the human population over the last century, especially due to resource-intensive agriculture in the developing and underdeveloped world, with the sector now accounting for 70 percent of global freshwater use.[2] The forces of global warming and climate change, too, have exacerbated the global water crisis by causing a shift in ecohydrological cycles, resulting in spatial and temporal variabilities in precipitation and temperatures.
The Malthusian creed associates conflicts over natural resources with their relative or absolute scarcity.[3] The Food and Agriculture Organization (FAO) classifies water scarcity into two classes: physical water scarcity and economic water scarcity.[4] The former is the lack of physical availability of water to meet various demands, while the latter is generally a characteristic of arid regions. Additionally, overallocation and overdevelopment for supply augmentation through structural engineering can fragment water systems and create artificial scarcity in semi-arid or non-arid regions as well.[5] Physical water scarcity manifests as severe environmental degradation and increasing occurrence of conflicts, and it arises primarily due to either a shortage in the quantity of usable water (i.e. drinking water and water used for other purposes) or an extreme spatial disparity in water distribution—i.e. certain regions endowed with greater amounts of water (e.g. western Europe, US east) than other regions (e.g. sub-Saharan Africa). In a temporal context, there are three additional notions of scarcity, the first of which is related to annual fluctuations in water availability where the physical availability of water in a particular region diminishes during seasons of low precipitation. The second notion is concerned with population growth, where enhanced economic activities lead to diminishing per capita availability of water over time. This situation is exacerbated by rapid urbanisation and industrialisation. Thus, the demand for water is likely to increase further in the near future, intensifying the existing problems. The third is related to climate change, which can cause problems by shifting the precipitation regime.
Economic water scarcity, meanwhile, is a result of lack of access to water rather than diminished physical availability. This is often due to a lack of investment in water infrastructure or inadequate infrastructure development, resulting in economic agents being deprived of water for economic use (e.g. agriculture, industry, households); high susceptibility to seasonal, annual and long-term fluctuations to the physical availability of water; and inequitable distribution of water even when infrastructure exists.[6]
In contrast to the Malthusian creed of scarcity propounded by the FAO, the paradigm of Integrated Water Resources Management (IWRM) recognises the ecosystem as a critical stakeholder in the water-demand matrix. To combat economic and physical scarcities, the erection of supply augmentative structures (e.g. dams, barrages, diversion channels) emerged as the dominant paradigm, with more water diverted to the water-scarce zones from the water-rich zones, through interventions in the natural hydrological flows.[7],[8] However, despite the initial short-term successes, over time, it became evident that the new and emerging challenges of the future could not be resolved by addressing scarcity alone. A strategy focused exclusively on increasing interventions into the hydrological cycle came to be regarded as counter-productive because of the adverse impacts on the basin ecosystem. Consequently, policy documents as well as actions in the developed world, began to focus on holistic approaches to managing water and governing river basins, triggered in particular by ecological concerns.[9]
Successive dam decommissioning is testimony to this shift in paradigm, which renders higher priority to projects that meet basic and unmet human and ecosystem needs for water.[10] Thus, in the IWRM paradigm, the conflict between economic demands and ecosystem demands for water are duly acknowledged. In that sense, “scarcity” is not merely a human economic issue but can be a characteristic of the ecological sector, especially when supply-augmentation plans for meeting unbridled human demands can fragment river systems; impact the integrity of the basin ecosystem; and cause irreparable ecosystem destruction, affecting the provision of ecosystem services in the long run.
The biggest withdrawals of water from the natural ecosystem occur in the agriculture sector, primarily for irrigation. According to the World Bank, while agriculture accounts for an estimated 70 percent of total freshwater withdrawals globally, water withdrawals in the arid and the semi-arid regions account for more than 90 percent of total consumption.[11] In many cases, therefore, water conflicts are not always a function of the physical scarcity of water but are a temporal coincidence of demand, based on the scarcity value of the resource.[12] A mathematical model by Ghosh and Bandyopadhyay[13] reproduced in this paper delineates the scarcity value of water as the marginal value loss due to the scarcity of water. The magnitude of the loss is a metric of the degree of deprivation and creates the basis for water conflicts.
This paper aims to show how water futures trading can help arrest scarcity in a water-scarce economy, arguing that in such economies, water futures trading can compensate for the loss incurred by an economic agent under various scenarios. The paper makes a case for the increasing utility of such trading in the context of climate change and associated water-availability variability in two situations: first, where water futures trading co-exist with physical trading (the case of western US); second, where both physical markets and futures markets are non-existent (the case of India).
The rest of the paper presents the theoretical setting through a static mathematical framework of scarcity value of water, and the loss function associated with scarcity; discusses the benefits of water futures trading; explores how the NASDAQ Veles California Water Index futures contract can help the farm community amidst a long-running drought; and outlines the problems specific to India and how water futures trading can help address the increasing water-availability risks.
2. “Scarcity Value” in Water-Scarce Economies: The Theoretical Setting
This section presents the mathematical model to understand the notion of the scarcity value of water in a water-scarce economy, as delineated by Ghosh[14] and Ghosh and Bandyopadhyay.[15] This model assumes that the scarcity value that arises in a water-scarce economy can be a result of either physical scarcity or economic scarcity, or a combination of both. Thus, scarcity value can reflect both physical and economic scarcity. Further, the scarcity value of the ecosystem services of water is not captured in this model, with the assumption that addressing the scarcity value of water in the economic sector will organically address the scarcity value of the ecosystem services associated with natural flow regimes. Additionally, the framework is confined to agricultural scarcity value, for the following reasons: a) 90 percent of water withdrawals occur in the agricultural sector in large parts of arid and semi-arid zones; b) a majority of the cases of water disputes can be attributed to agricultural water use; c) water disputes in large parts of the arid and semi-arid world occur because of scarcity, leading to losses in agricultural production.
The model rests on two basic assumptions.
Assumption 1: Water’s only value lies in the economic returns it yields. This postulate, in line with Fisher and Huber-Lee,[16] asserts that the stakeholders’ interest in water lies with its economic value. This implies that the economic value loss due to water scarcity (physical or economic) can be compensated monetarily or through other means.[17]
Assumption 2: Ceteris paribus, water from one source, is substitutable with water from any other source. This postulate implies that if water is obtained from source X, then the value of water from source X will diminish for the stakeholder if it finds another source of water, Y. This assumption is again based on the idea that the value of water is derived solely from its economic use.
Another postulate, which is an integral characteristic of the definition of water-scarce economies, is incorporated.
Assumption 3: Water scarcity constrains land use. It is assumed that land is available in abundance in the short run. While hectares can be brought under the production process if water is available, the unavailability of water can constrain land use. This also implies that other factors of production are not constraining factors in this classification of a water-scarce economy, leading to the next postulate.
Assumption 4: Ricardian rent is discarded. Though Ricardian rents might arise in the process due to land quality differentials (reflected in yield differentials), it has been kept out of the purview of this analysis.
It is important to note that unless water availability increases, the area under production for the crop under consideration cannot be increased. This leads to an alternative definition of a water-scarce economy: A “water-scarce” economy is one that constrains land use due to scarcity of water. This also leads to the inference that a “water-scarce” economy is one where water-supply augmentation is associated with increases in agricultural land, as water remains the only binding factor for bringing more land under agriculture.
2.1 The Model
Based on the above assumptions, the model will consider a hypothetical agrarian, “water-scarce” economy, steamrolled into a farm. Water is the only input in the production process and makes up the production function, with a representative crop grown in the economy. The farmer maximises their surplus return or profit in terms of water use, which is the binding factor here. The farmer will use water till the point where their profit is maximised. The variables used are as follows:


This implies that even if extra units of land are brought under the fold of the production process, without an extra unit of water for each extra unit of land, nothing can be grown. Thus, area can act as a good proxy for water use, or the other way round.
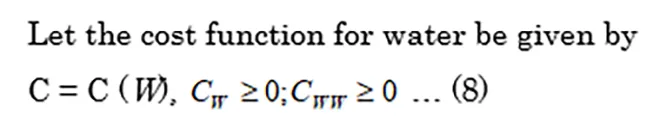
This cost function can be construed as the cost emerging for accessing water, monetised or otherwise. This may also entail the externality cost if the same can be computed, as well as the opportunity costs of all forms to the extent perceptible and estimated. Since production is expressed in real terms (i.e. in terms of the product and not the value of the product), the cost can also be expressed in “real” terms. This has already been done in an earlier exposition of the scarcity value model.[18]
The surplus or the profit created therefore is the difference between the production (given by (2)) and the cost function. The surplus is denoted by:
Π (W) =F (W) – C (W) … (9).
As stated earlier, irrespective of the assumption of a perfectly competitive product market, where the producer is a price-taker, this model expresses profit or surplus function in real terms. Both marginal product and marginal cost have been expressed in terms of the product, not in terms of the money.
In the hypothetical economy, the profit, as expressed in (9), is being maximised subject to the water-availability constraint (4). In optimisation terms, this entails the creation of a Larangian L in the following form:
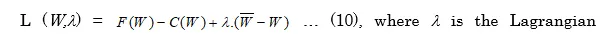
The Kuhn-Tucker conditions yield the following as shown in (11) and (12).

The Lagrangian multiplier in (10) is the shadow value of water.[19] It denotes the extent to which the surplus can be enhanced, if the constraint on water availability is released by a unit. As shown in (13), at the equilibrium, this is given by the difference between the marginal product of water (FW) and the marginal cost of water usage (Cw). This is what has been defined as the “scarcity value” of water (See Figure 1).
Fig. 1. Scarcity Value of Water Resources
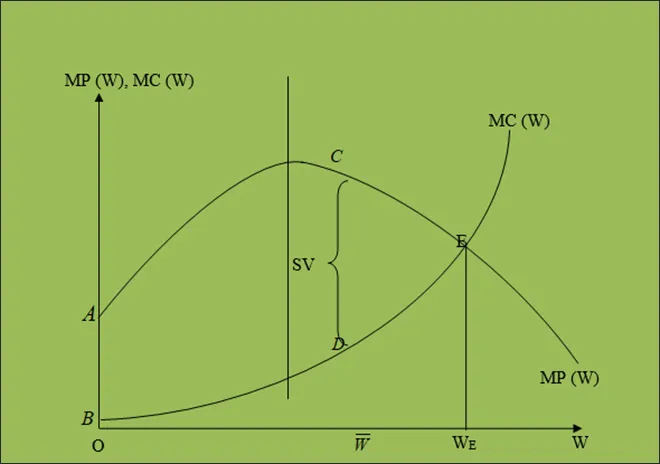
Thus, under conditions of perfect competition, profit-maximising producers will produce till the point where the value of the last unit produced (marginal product) is equal to the cost incurred for the last produced unit (marginal cost). In terms of (13), this would have implied. In Figure 1, the horizontal axis shows the water axis (W), while the vertical axis is the value axis.
However, in a water-scarce economy, due to availability constraints, . As with any other input in a well-behaved production function, it is assumed that the value of the marginal product of water is positive (possibly initially increasing) and diminishing, while the marginal cost function is increasing. The former is given by MP(W), while the latter is given by MC(W) in the diagram. Under conditions of producers’ equilibrium, the producer produces till point E, where MP(W) intersects with MC(W). The water usage till that point results in the equilibrium water usage and is given by WE in Figure 1. Furthermore, since the functions are “well-behaved,” i.e., the second-order condition for maximisation will suggest that the optimiser operates at the diminishing component of the MP(W) curve and the increasing component of the MC(W) curve. This paper does not delve into the second-order conditions, which are axiomatic.
Due to the scarcity of the resource under consideration, the maximum availability of water is given by the vertical line emanating from , which denotes the resource constraint. This amount is less than the equilibrium quantity. The difference between the MP(W) line and the MC(W) line is the reflection of the extra value that could have been obtained with a small increase in water availability. The distance between the marginal product and marginal cost is defined as the scarcity value of water.
Thus, if S (ϖ) denotes the scarcity value as a function of the constraint line , then
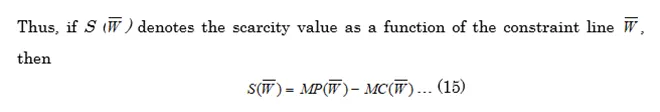
This gap is given by the length CD (See Figure 1). To reinterpret (15) in the context of Figure 1, it can be made out that a rightward movement of the line (or relaxation of the water-availability constraint) will reduce the length of CD (or the gap between and , implying a decline in the scarcity value.
2.1.1 The Loss Function
The loss function is delineated in the context of the water-scarce economy emerging out of the scarcity values. Assuming that the loss function is denoted by γ, it is already stated that the producer would have opted to operate till point E in Figure 1, where water use is WE. In that case, the producer obtains a net surplus given by:

2.2 Attempts to Reduce Scarcity Value and Loss Functions
The loss function CDE is a positive and increasing function of the scarcity of water, given by the line CD. Economies have attempted various ways to reduce this loss function, by trying to reduce the scarcity value of water. Most of such attempts have been supply-side. While they have led to short-term resolutions, these efforts have also created problems in the long run. Thus, recent efforts have involved institutional-level approaches and demand management. Global best practices have often focused on demand management using technological,[20] economic (including pricing of waters, virtual water imports),[21],[22] and practice-oriented (system of rice intensification, saturated soil culture, and alternate wetting and drying) methods.
This paper examines how derivatives markets for water can help in reducing the scarcity value and, eventually, the loss function. It makes a case for water-derivatives markets and, more specifically, the water futures market
3. Benefits of a Water Futures Market
There are various expected benefits of the water futures markets.[1] First, trading in water futures will help in price discovery and create a benchmark price for critical water-related decisions in the water-scarce economy. An efficient futures market should reflect on the scarcity value of the resource through these prices to aid efficient allocation and distribution.[2]
Second, the water futures price, under efficient market conditions, emerges as a price and scarcity indicator for the future. This will assist investment decisions as well as forward risk management under conditions of water-availability variability.[23], [24]
Third, the price discovered in the futures market can help with the impact assessments of water infrastructure projects or other infrastructure projects that can impede on existing flow regimes. Often, when there is more than one project, a choice must be made between them. The futures price discovered under supposedly efficient market conditions can provide a quantified basis for ranking projects, which will help in the decision-making process. In a water-scarce economy, with agriculture being the dominant user, the futures price of water will be decisively influenced by the scarcity value of water in agriculture.
Fourth, the pricing of water can raise public and political awareness of not only the importance and availability of the water but also the importance of the basin ecosystem that provides the water. This also corrects for market failure of water, especially when valuation mechanisms are absent. For example, the absence of a formal physical market for water in South Asia prevents the scarcity values of water from being expressed in an institutional framework. A futures market (even where physical markets are not allowed to operate formally) by discovering prices, can indicate the scarcity value of the resource, based on future availability, to create public, policy, and political awareness on how to manage an impending crisis under looming water scarcity.
Fifth, in large parts of the agrarian world, there are few potent risk-management or hedging instruments that can protect a fledgling agricultural sector from water-availability vulnerabilities. The futures market enables both irrigated and rain-dependent agriculture stakeholders to insure themselves against droughts, by locking in prices. This occurs through a risk transfer to the speculators and private players, and enables the lowering of the scarcity value of water (equation [15]) and compensating for the loss function (equation [18]). Consequently, the burden of drought relief currently borne by governments is significantly reduced.
Sixth, water futures trading provides a necessary hedging tool to investors, refinancing institutions, and agri-finance corporations, to hedge their investment and loan risks. Additionally, banks and financial intermediaries can develop other products suitable for their customers by making use of the water futures market.[25]
Seventh, a water futures market can help promote technological innovations in the water sector. Since most important element is information development and data processing/mining and infrastructure, there will be more investment in information-gathering and decision support system tools for water. This will encourage further research on water resources and will eventually help in future crisis management.
The futures market can play a very important role in decision-making related to water in water-scarce economies. At the same time, it can also ensure just distribution and safeguarding conservation priorities, especially where water must be kept instream for ecosystem needs, by compensating the community for not using water.
The range of beneficiaries of water futures trading is not confined to the agricultural sector. Corporations producing hydropower may also benefit from it, as also municipal corporations, municipalities, and water boards who can also hedge positions in the futures exchange for water and may use the funds for infrastructure development to improve urban services. However, since the agricultural sector accounts for the maximum usage of water, the most substantial impact of the futures market will be on the agricultural value chain (from farmers to consumers). Hedging in the water futures exchange will not only minimise the producer’s and the supplier’s risks by creating adequate compensations for loss, but also put the suppliers in a position to pass on parts of the benefits to the consumers. A futures market for water can thus act as a market-based “bail-out institution” for all the beneficiaries, thereby reducing the pressure on the government exchequer. The framework developed in this paper can easily be extended to urban waters by replacing the marginal production function (as described in section 2) with a marginal utility function. In the case of hydropower or industrial water use, the marginal product function is valid, but with changing functional characteristics.
4. Water Index Derivatives Trading in California
The Colorado basin states in the western US are experiencing an unprecedented water crisis, which has been described as a “historic long-term drought.” By mid-August 2021, the US Bureau of Reclamation had officially declared a severe water shortage at Hoover Dam’s Lake Mead, the largest reservoir in the US. While the Lake Mead was barely 35 percent full, the lowest since its construction in the 1930s, the second-largest reservoir in the Colorado basin, Lake Powell, recorded water levels at 32 percent of its full storage capacity. Such low runoff conditions have led to substantial reductions in downstream releases from Glen Canyon Dam and Hoover Dam in 2022 due to declining reservoir levels, resulting in mandatory reductions in water allocations for all the three lower Colorado states—California, Arizona, and Nevada—as well as for the downstream nation of Mexico. Based on the federal guidelines worked out for combating drought conditions in 2019, Arizona’s allocation from Lake Mead declines by 18 percent, while those of the state of Nevada and the nation of Mexico declines by seven and five percent, respectively. Nevada has already reduced its deliveries to combat the scarcity conditions. According to NOAA (National Oceanic and Atmospheric Administration) drought outlook,[26]drought conditions are expected to persist in the West, which is already amidst a decades-long megadrought, through 2022 and beyond.
The long-term trend of the Colorado system reveals a decline in the run-off, which has largely been attributed to the forces of human-induced climate change. A recent paper in Science[27] claims that, in the Upper Colorado system, a degree increase in temperature is associated with a 9.3 percent annual mean decline in discharge due to enhanced evapo-transpiration, mainly driven by snow loss and a consequent decrease in the reflection of solar radiation. There are numerous historical accounts of river development based on a structural engineering paradigm, in response to increasing water demand in the western US, causing serious long-term negative effects on the environment and water quantity.[28], [29] The decline in long-run run-offs has often been attributed to the fragmentation of the flows caused by multiple constructions for storages and diversions, especially during the so-called “dam-building decades” of the 1920s to 1960s.
Given such deleterious impacts of these constructions, over time, the US began decommissioning dams and adopted various demand-management measures through compacts and statutes, the latest being the one from 2019. Interestingly, physical water markets through spot trading emerged in California as a response to the declining water availability. In this market, short- and long-term leases, as well as permanent water rights, are traded. Such trading enhances flexibility in water management, with prices discovered in the physical markets helping in ascertaining the value of water. Around 1.5 million acre-feet of water is traded annually, accounting for about four percent of all water used by cities and farms.
The most interesting intervention emerged in December 2020 with the CME Group and NASDAQ launching the NASDAQ Veles California Water Index Futures Contract. The derivative contract is designed for California, which is endowed with a highly liquid and buoyant physical water market worth more than US$1.1 billion as of 2019–20. The futures contract is associated with the spot market price underlier in the form of Nasdaq Veles California Water Index—a price index estimated as the volume-weighted average price of water calculated based on the transaction prices of water rights in California’s five most liquid markets. As against physical delivery, these futures contracts are financially settled, allowing for better leveraging and reducing the transaction costs including those of delivery. The California water futures contract is designed to help water users in the state hedge the risks associated with California’s ever-changing hydrological situation, fuelled by the volatility in physical water availability in the lower Colorado system, which is reflected in the volatilities in the physical market prices.
The index constructed on the basis of the physical market prices is updated weekly by NASDAQ, under the name NQH2O. The price differential between the weighted index of the price and the actual transacted price is known as the basis, and the basis risk might prevail if the movement in the index across time is not correlated to the physical price movements. This, of course, creates opportunities for speculative trading. The contract size is 10 acre-feet of water, with the maximum maturity period being two years. The broad classification of the participants in the California water futures market can be divided into two (like any other futures market): hedgers and speculators. As defined, hedgers are those directly connected with the physical use of the resource or are indirect stakeholders (e.g. municipalities, water districts, and businesses such as farmers or manufacturers, banks and financial institutions whose risks in the forms of farm loans are linked to water). Speculators are individuals or companies looking to make money on the market by betting on the future price of water. Speculators are not exposed to the risk of physical water availability—neither through their loans nor investments. This category often includes wealth-management firms, hedge funds, or other financial companies that may be interested in portfolio diversification.
Box 1: A Hypothetical Example of Hedging Using Water Futures in California
|
Consider a California vineyard owner who, in January, hedges the risk of water scarcity by taking a “long” position and buying 10 water futures contracts, equivalent to a total of 100 acre-feet of water, at a contract price of US$800 per acre-foot. By the beginning of July, the contract price according to the NQH2O index rises to US$1000. This price rise can happen under conditions of scarcity, based on the physical market conditions. Under such circumstances, the vineyard owner can square off the position in the futures market, and gains the difference of his buying price and current price, i.e. US$200 per acre-foot, a surplus of US$20,000. This can help the vineyard owner in two ways. First, they can use this amount to minimise the loss that occurred in their wine business due to water scarcity. Second, they can use the surplus to purchase physical water from California’s water markets to maintain the same level of wine production and revenue. Thus, the vineyard owner has successfully hedged the water risk by participating in the California water futures market and been compensated for the loss function given by the equation (18) or area CDE in Figure 1.
Even during conditions of “no scarcity,” the futures market will be helpful for the farmer. If the NQH2O index price declined to US$600 per acre-foot in July, due to excess water availability, the vineyard owner squares off the position with US$200 per acre-foot of loss, with a total loss of US$20,000. However, this is compensated as he saves roughly the same amount in the physical market, since the physical market price of water has also gone down by a similar extent. In that sense, the owner will be in a “no loss, no gain” situation assuming they take equal and opposite positions in the futures and physical markets. Therefore, their participation in the futures market offers the vineyard owner much-needed stability in planning and acts as an insurance mechanism against risks associated with water availability and prices.
|
Some recent frameworks[30] have predicted water availability in the Colorado system with reasonable precision, especially through a drift-free decadal climate prediction system using a fully coupled climate model. However, that does not take away the risk associated with water availability. This is where a water futures market is important. In the present scheme of things, this phenomenon of water futures seems to be confined to California, and the index may not be reflective of the situation in other parts of the western US. The current problem of drought can aptly be described as a “basin-wide regional common”: it affects all states, all sectors, and all stakeholders negatively, albeit in varying proportions. Thus, all the states eventually need such an instrument. More importantly, the futures contracts must be designed based on the needs of the states, since the levels of scarcity are variable. If market prices are to reflect the scarcity value, then a California-specific contract may not accurately reflect the drought situation in Upper Colorado or even Nevada and Arizona.
5. A Case for Water Futures Exchange for India
The water-availability risk in India is acute, especially due to shifting precipitation regimes as well as variability in precipitation quantities. However, there is no market in India or South Asia where users and investors exposed to water-availability risks can effectively hedge against them. This is now becoming a cause for concern, especially in light of the climate variability in the region, since a large part of South Asian agriculture is dependent on precipitation from the Southwest Monsoon (June–September). Data from the Fertiliser Association of India, for 35 select districts across the country, shows that the precipitation in India from 1989 to 2009 fluctuated between 77 percent (worst case) and 119 percent (best case) of normal rainfall (defined by long-term average value).
The unpredictability is also noted across the measuring stations across river basins in India. Table 1 shows the mean, standard deviation, and coefficient of variation of precipitation in Gangetic West Bengal and the South Interior Karnataka that lies largely in the Cauvery basin. The observations are based on area-weighted monthly rainfall, which has been used to estimate the precipitation during the high monsoon months ranging from July to September in Table 1.
Table 1: Mean, Standard Deviation, and Coefficient of Variation of Area Weighted Precipitation during July–September
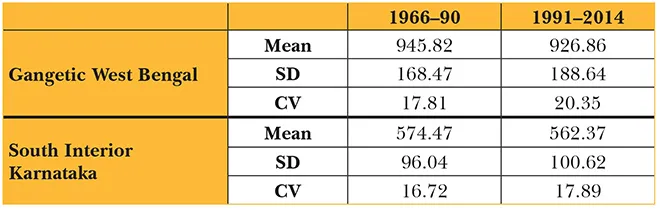
Source: Computed by author on the basis of data from Indian Meteorological Department.
For both Gangetic West Bengal and South Interior Karnataka, the mean precipitation declined during 1991–2014, compared to 1966–90, while the standard deviation increased. Thus, while precipitation has declined, the variability in rainfall has increased in the second period as compared to the first period. This is reflected in a higher coefficient of variation in 1991–2014 for both regions. Thus, precipitation has been unstable and on a decline.
The failure or shortage of precipitation often leads to water shortage in reservoirs, leading to their failure to release water to agricultural fields in a timely manner. This affects food production and creates water conflicts, for example, the Mettur Dam in Tamil Nadu and the conflict between upstream Karnataka and downstream Tamil Nadu over Cauvery waters. The first barrage to receive water from the Cauvery in Tamil Nadu after the river crosses the Karnataka boundary is Mettur. A failed monsoon or less water from headwaters may lead Karnataka to release a quantity that might be less than what is stipulated by the Cauvery Water Tribunal in its Final Order of 2007. Historically, this has frequently fuelled serious interstate water disputes. Figure 2 shows the temporal movement of water flow to Mettur Dam above the 2007 allotment in TMC, and the deviation from 25-year mean precipitation in the southwest monsoon months of the years between 2007–08 and 2014–15. A regression analysis also shows that monthly precipitation in the South Interior Karnataka is a statistically significant variable (at five percent), explaining the flow to the Mettur dam.
Figure 2: Flows to Mettur Dam above the 2007 Allotment (TMC), and Deviation from the 25-year Mean Precipitation in the Monsoon Months of the Year between 2007–08 and 2014–15
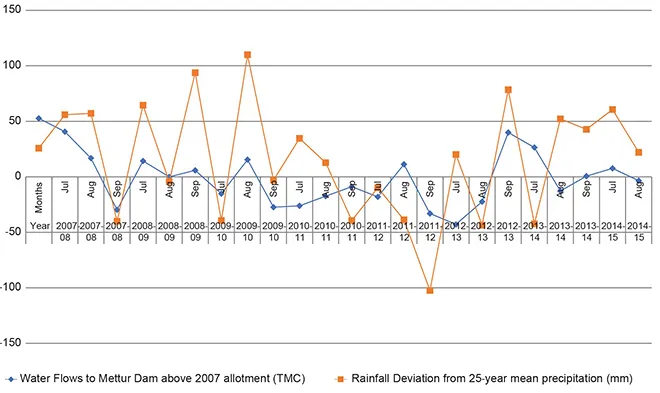
Source: IMD and Cauvery Technical Committee Report to SC, Volume 1, Main Report, New Delhi, October 2016.
The above case exposes the existing and emerging risks in water availability that pose a threat to food security and various activities, endeavours, and businesses around agriculture. To mitigate such risks, supply augmentation plans through constructions of storages and some demand-management mechanisms have been proposed. Yet, none of the current risk-mitigation strategies financially compensate for losses incurred due to water shortage. Thus, there is value loss due to the unavailability of water, as well as loss incurred due to the cost of adaptation (through the shifting of crops or construction of storages). Informal water forward markets are in vogue to a certain extent in many parts of South Asia, but they have not been successful in mitigating the risk of water availability at the river basin level. This leaves the entire agricultural value-chain—including intermediaries, final consumers, lenders, banks, insurers, and reinsurers—exposed to the risks. To address this gap, India must consider implementing a water futures trading contract.
5.1 Development of the Water Index Futures Market: The Water Availability Index
India has no formal physical spot markets at the levels of river basins or states. Consequently, there is no physical price mechanism for which a price index can be constructed. The obvious question then is: On what basis can we propose a futures contract? The answer lies in the development of a “Water Availability Index” (WAI). Such an index must be independently and objectively priced, with minimum scope for artificial manipulation. The idea is to develop a contract for each major river basin in a given state. For example, there might be two contracts based on two indices on the Cauvery Basin—one for the water stored in the barrages or reservoirs within the borders of Karnataka, and one for the water stored in the barrages or reservoirs within the borders of Tamil Nadu. Previous research has shown that water within each boundary has traditionally shown different scarcity values, despite being part of the same basin system.[31]The hydro-politics of the region increases the risk faced by the farmers in downstream Tamil Nadu, though contingent upon a few common broad climatic factors, with water during the dry season being a “zero-sum” game. The lean season has often witnessed a situation in which upstream Karnataka has not been able to release adequate amounts of water (See Figure 2). A common index for the Cauvery Basin will not reflect the ground reality. Thus, there is a need for different state-specific indices for farmers and other stakeholders to hedge their risks.
Table 2 shows the various barrages, their capacities, and the actual storage on the four dams in the Cauvery Basin in Karnataka on four selected days—between 15 October and 3 November 2021. The four dams are Harangi, Hemavathy, Krishnarajasagara, and Kabini. The index represents the actual storage in the node (consisting of the four barrages, in this case) as a percentage of “full capacity.” The index moves up and down in response to the actual water stored in the four dams, representing the node here. The maximum index value is 100, and the minimum index value is zero. As storage increases in response to water inflows, the respective index will also rise.
Table 2: WAI Status in the Cauvery Basin in Karnataka
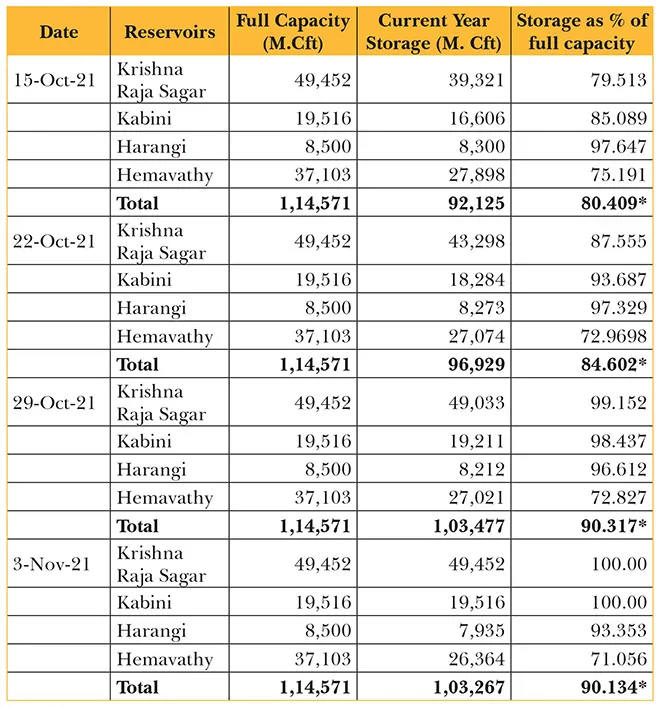
*indicates the value of the WAI.
Source: Author’s computation using data from http://122.15.179.102/ARS/home/reservoir/2021-11-02 (last accessed on November 3, 2021).
5.2 WAI and Scarcity Value of Water
As argued earlier, scarcity value depends on both demand- and supply-side parameters associated with the excess demand for water. Additionally, it responds to water pricing. Previous exercises, namely by Ghosh[32] and Ghosh and Bandyopadhyay[33], estimated the scarcity value of water in the Cauvery Basin over time and across seasons, with scarcity value defined as “loss of rice production per unit of water,” in terms of the model shown in Section 2. Based on those estimates, this paper shows the correlation coefficient of the WAI with the scarcity value of water for two agricultural seasons (Kharif and Rabi) for the Cauvery–Karnataka node.
In this case, considering the minimum support price for paddy, the scarcity value has been expressed in rupees per cubic metre of water. For all practical purposes, the choice of crops will not have an impact on the hedging activity; it is the loss function that gets compensated in this case. This demonstrates how futures trading can help even without the existence of physical markets. While in the Californian case, the futures market is an appendage of the physical market and helps in hedging the price risks, in the Indian case, the futures market can act as an insurance product to hedge against the possible losses. The movement of WAI for the Kharif season for the Cauvery– Karnataka node is, of course, a function of the success or failure of the monsoons. This is clear from the fact that in 1995 and 1998, rainfall in the Cauvery Basin was less than usual, as documented by Ghosh, which also resulted in lower WAI.
The scarcity value of water in the Cauvery–Karnataka node for Kharif rice had increased, reflecting an increasing demand for water in the basin. An improvement in WAI cannot always be associated with a reduction in the scarcity value; here, since more area had been brought under paddy cultivation (the most water-consuming crop in the region) during this phase. However, in 1999 (a year of bad monsoon), the sharp decline in WAI has been associated with a sharp rise in scarcity value.
To be sure, Kharif paddy is less dependent on irrigation compared to other crops of rice. Thus, while a negative and significant correlation exists between WAI and scarcity value for the Kharif season (that is –0.65), the correlation coefficient is not as strong as being in the high range of –0.9 or above (See Table 3), as is the case for Rabi.
Table 3. Correlation Coefficient of Water Availability Index and Scarcity Value (Kharif) in the Cauvery–Karnataka Node

** Significant at one percent level.
As estimated between 1992 and 1998, WAI moved between 0.8 and 0.9, while SV had moved between INR 0.4 per cubic metre and INR 0.6 per cubic metre. However, a drop in WAI to around 0.71 in 1999 was associated with a sharp increase in the scarcity value to INR 1.31 per cubic metre, i.e. a more than double increase. The correlation coefficient between WAI and SV of water for Rabi rice is as high as –0.92 (See Tables 4 and 5).
Table 4: Correlation Coefficient of Water Availability Index and Scarcity Value (Rabi) in the Cauvery–Karnataka Node

** Significant at one percent level.
In both cases, the correlation coefficient is negative and significant at one percent. However, the negative relation is stronger for Rabi, compared to that for Kharif. Rabi paddy is entirely irrigated, while Kharif paddy’s growing season merges with the Southwest Monsoon. Thus, the correlation between the SV of water and the WAI (based on the water stored in reservoirs), despite being negative, is not very high. On the other hand, the Rabi crop depends on irrigation, and a low WAI will result in high scarcity value. This adequately matches with the theoretical explanation of the scarcity value of water provided in Section 2.
An efficient market is one where prices reflect the scarcity value. Therefore, the prices in the markets where such indices will be traded are supposed to reflect the scarcity value of water. If the markets are efficient, one may safely assume that the price sensitivity of the water index (or the elasticity) will be high during dry periods, particularly for irrigated crops. Thus, an efficient index in an efficient market can be price sensitive.
In India, the futures contract can be developed for various nodes of various river basins, depending on the boundaries of the states and the locations of the reservoirs over the river basins. This can also help the non-agricultural sector, contingent upon certain other factors that are not within the scope of this paper.
Box 2: Using Futures Market to Hedge Water-Availability Risk
|
This is a hypothetical case of compensating for the “loss function” (See CDE in Figure 1), by participating in water index futures markets. Consider a farmer in the drought-prone Birbhum district in West Bengal who decides, in January 2022, to plant paddy in May 2022 on the expectation of good monsoon during June–September 2022. However, the threat of a failed monsoon looms large in his mind, since it will lead to crop failure and possible losses. He calculates that the loss from a failed crop will be INR 1 lakh, while the profit from a successful crop will be INR 5 lakh.
If it is assumed that the current level (January 2022) of the WAI in that node of West Bengal over the Ganges is 70.2 percent, with August 2022 water futures contract trading at INR 50 on the expectation that there will be good rain during the Southwest Monsoon, the WAI will increase to around 85 percent. The farmer, therefore, decides to buy 200 August 2022 WAI Farakka node contracts (the water of the Ganges gets diverted to resuscitate the Kolkata port through the Farakka Barrage in West Bengal, which was constructed in 1975) at INR 50. The existence of margin can be ignored for the time being.
Scenario A: Drought prevails due to the failure of the Southwest Monsoon, and the paddy crop fails. The WAI goes down to 50 percent, with its price increasing to INR 100 during expiry. As the contract expires on a particular day in August, the farmer cash-settles his position and earns a profit of INR {200 x (100-50)} = INR 100,000, thereby recovering the loss incurred due to a failed monsoon.
Scenario B: If there are good monsoons and WAI crosses the 85 percent mark, the farmer earns a profit of INR 500,000 by selling his crop. On the other hand, because the WAI is also high, with its price declining to INR 25, on the day of the expiry of the contract, the farmer incurs a loss of INR {200 x (50-25)} = INR 50,000. But this loss gets adequately offset by the profit earned by selling the crop.
Overall, participating in the water futures market allows the paddy farmer to have his “loss function” (given by CDE in Figure 1 and by equation [18]) compensated. Similarly, stakeholders such as banks, development financial institutions, hydropower producing units, and institutions providing agricultural credit may hedge against the vagaries of water-availability risk. Such hedging will, eventually, even out profits and losses by minimising the uncertainties in the outcomes. This mode of hedging is already prevalent in commodities; however, hedging in the context of water should be treated more as hedging in “inputs” rather than hedging in “outputs.”
|
6. Conclusion
Previous research has shown that the neo-Malthusian creed of resolving water-scarcity problems through supply augmentation plans is being challenged globally, with demand management options taking centre-stage. The scarcity value thesis posits that water conflicts are a function of the scarcity value of water, not of the physical scarcity of water. Therefore, efforts to reduce the scarcity value of water must be mainstreamed in water-governance frameworks. This paper argues that water futures trading through indices can help in reducing both scarcity value and the consequent loss function.
Since the idea of water futures is still nascent, it has rarely been discussed in contexts where there are no organised physical water markets. In India, the primary reason why formal markets for water do not exist in India is the idea that creating such markets will be exploitative for farmers. Indeed, in a country where agricultural inputs involving water is largely subsidised, it is difficult to argue in favour of market forces. However, this paper argues that water futures can help reduce the scarcity value of water, even in the absence of such a market.
At a time when the government is challenged with creating safety nets for the agriculture sector, especially against the vagaries of climate change, futures trading in water offers the unique opportunity to cater to the insurance needs of the sector—benefitting both the government and the private players. It can ease the pressure on the government exchequer (created by transfers or subsidies) and will be a market-based hedging instrument that can be used as an insurance product for the farm sector. More importantly, the gap created by the failure of weather insurance, due to lack of penetration, can be bridged by water futures trading. Within this framework, aggregators and other players in the farm value chain should act as direct participants, while the farmers will be the indirect beneficiaries of the process. This is important, since the small and marginal farmers in India have neither the capacity nor thewherewithal to trade in complicated financial instruments. Indeed, it may prove counterproductive for them if the right position is not taken in the markets in the absence of adequate market intelligence and decision support systems.
The paper has presented two distinct cases of water futures trading: one that already exists (i.e. California) and one that does not (i.e. India). Water futures trading in California occurs in the form of a price index derived from physical markets. This has been made possible due to the existence of a buoyant physical market of water. Thus, one of the major functions of the NASDAQ Veles California Water Index futures is that it helps the farm community or the hedgers to hedge against the physical market price risks. Under efficient market conditions, the scarcity conditions are reflected in the market prices. In India, where no organised physical market exists, the Cauvery-Karnataka futures contract is a good case study of how futures markets can help. In both cases, water futures trading helps in reducing the scarcity value of water and compensates for probable losses. Further, water futures trading can act as a market-based insurance mechanism under scarcity conditions. If the farm community, banks, financial institutions with substantial exposure (by providing loans to the farm community), insurers, and reinsurers have their risks associated with water availability, then water futures trading can be an excellent hedging mechanism for them by protecting their bottom-line and getting compensated for their losses (caused due to drought conditions) through such cash-settled futures contracts.
This paper has not delved into the regulatory aspect of the futures markets as far as India is concerned. There is no doubt that if such an instrument is traded, it will require a sophisticated knowledge base on the part of the regulator. A trans-disciplinary knowledge base for water-resource economics, institutions, and hydrological engineering must be created, and the regulatory authority’s expertise should not only be confined to the working of the markets but should also extend to an understanding of the trans-disciplinary knowledge base as well as regulatory problems. Further, the regulatory authority should consist of specialists in various aspects of water-resource management, not just bureaucrats.
At the same time, it is important to make information on all water-related aspects publicly available, and develop adequate analytical methods and instruments for better predictions. Equipped with adequate information, an efficient futures market for water can help in discovering the price of water, which will reflect the scarcity value of the resource. While the nature of the contracts in the US is fundamentally different from what is proposed in India (the former being a tradable price index, the latter, a quantity index), there are lessons to be drawn from the US experience. Much like the NASDAQ Veles California Water Index futures, the Indian contract should also be cash-settled, instead of relying on the physical delivery of the resource (unless a hedge has been rolled over). The cash-settled price will reflect the scarcity value of water, thereby ensuring price discovery. This will ensure the liquidity of the contract under consideration as well as compensate for the “loss function” incurred, thereby helping resolve water-related conflicts. Finally, the social implications of futures trading in water are also far-reaching. It can reduce the social cost of water conflicts by compensating “loss functions” of the water stakeholders, and also help in wealth creation, thereby boosting regional development.
Endnotes
[1]Futures markets for water essentially involve trading in a standardised contract in an exchange platform, and are paper markets used for hedging the price risks, or for speculation, and generally preclude physical delivery of the underlier (i.e. water, in this case). However, in large parts of the developing world, including South Asia, there are forward markets for water that are used to contracts that provide for the physical delivery of a commodity. Such forward agreements are customised contracts between two parties to buy or sell water at a specified price on a future date. Therefore, they too serve the purpose of hedging. However, due to their customised nature, they are hardly tradeable (and are not exchange-traded products) and may not always serve the purpose of price discovery, as the futures platform does.
[2]Even in the absence of physical or spot markets, the futures market can help in price discovery through the scarcity value route in the futures market framework. This has been exhibited in the Cauvery case examined later in this paper.
[1]World Water Assessment Programme (Nations Unies), The United Nations World Water Development Report 2018 (United Nations Educational, Scientific and Cultural Organization, New York, United States) www.unwater.org/publications/world-water-development-report-2018/. (2018).
[2] http://www.fao.org/aquastat/en/overview/methodology/water-use
[3] T. Homer-Dixon. “Environmental Scarcities and Violent Conflict: Evidence from Cases”, International Security 19(1) (Summer 1994): 5 – 40.
[4] http://www.fao.org/resources/infographics/infographics-details/en/c/218939/
[5] N. Ghosh.”Challenges to Environmental Security in the Context of India-Bangladesh Trans-boundary Water Relations”, Decision (Springer), 42 (2) (2015): 211-28.
[6] http://www.fao.org/aquastat/en/overview/methodology/water-use
[7] K.L. Rao India’s Water Wealth (New Delhi: Orient Longman, 1975).
[8] M. Reisner. Cadillac Desert: The American West and Its Disappearing Water (New Rork: Viking Books, 1993).
[9] Q. Schiermeier, “Dam removal restores rivers”, Nature, 557 (2018): 290-91.
[10] P.H Gleick, “The Changing Water Paradigm: A Look at Twenty-first Century Water Resources Development”, Water International, 25 (1) (2000): 127-38.
[11] S.M. Scheierling and David O. Tréguer. Beyond Crop per Drop: Assessing Agricultural Water Productivity and Efficiency in a Maturing Water Economy. International Development in Focus. (Washington, DC: World Bank, 2018). doi:10.1596/978-1-4648-1298-9
[12] N. Ghosh and J. Bandyopadhyay. “A Scarcity Value based Explanation of Trans-boundary Water Disputes: The case of the Cauvery Basin in India”, Water Policy, 11 (2) (2009): 141-67.
[13] Ghosh and Bandyopadhyay. “A Scarcity Value based Explanation of Trans-boundary Water Disputes”.
[14] N. Ghosh. Economics of Hostile Hydropolitics over Transboundary Waters: Scarcity Values and Interstate Water Conflicts in India and US (Saarbrucken, Germany: VDM Verlag, 2009).
[15]Ghosh and Bandyopadhyay. “A Scarcity Value based Explanation of Trans-boundary Water Disputes”.
[16]F. Fisher and A. Huber-Lee. Liquid Assets: An Economic Approach for Water Management and Conflict Resolution in the Middle East and Beyond. (Washington, DC: Resources for the Future, 2005).
[17]The implication here is that “wealth effects” are not prevalent. This implies that there always exists an amount of money or any other incentive that can make agents shift their choices from bundle A to bundle B, considering the definition provided by Milgrom and Roberts (1992). For details on this definition, please see: P. Milgrom and J. Roberts.Economics, Organization and Management (Prentice Hall, 1992).
[18] Ghosh. Economics of Hostile Hydropolitics over Transboundary Waters.
[19]The Lagrangian Multiplier: A Mathematical Interpretation of “Shadow Value”
The Kuhn-Tucker conditions yield the optimum values for W andl, as functions of P and .Hence, for the optimum values of W andl, I write the following:
W = W (P, ) … (3.14)
l = W (P,) … (3.15)
Hence, the optimum profit would be a function of P and , and can be represented as:
p(P, ) = P.F(W (P, ) ) –C (W (P,) … (3.16)
Partially differentiating p in(3.16) w. r. t.:
… (3.17)
Incorporating (3.9) into (3.17):
… (3.18) [as = 1]
The assumption of = 1 is based on the fact that any relaxation of ceiling on will witness the entire extra amount being used up in a water-scarce economy. The implication of (3.18) is that the extra unit water availability over the ceiling (or a relaxation of) increases the optimum profit by the extent of the lagrangian multiplier,l. This is the shadow value of the resource.
[20] B. Boumann, B. and T. P. Tuong. “Field water management to save water and increase its productivity in irrigated rice”, Agricultural Water Management, 49(1), (2001): 11–30.
[21] Ghosh and Bandyopadhyay. “A Scarcity Value based Explanation of Trans-boundary Water Disputes”.
[22] R. Saha and P. Kapuria. “Finding Solutions to Water Scarcity: The Potential of Virtual Water Trade in Agricultural Products”. ORF Occasional Paper No. 298, February 2021. Observer Research Foundation.
[23] N. Ghosh. “Conceptual Framework of South Asian Water Futures Exchange”. Commodity Vision, 4 (1), (2010): 8-18.
[24] Australian Stock Exchange. “Establishing a futures market in Water Availability Risk”. Discussion Paper, 2006.
[25] Australian Stock Exchange, “Establishing a futures market in Water Availability Risk”.
[26] https://www.cpc.ncep.noaa.gov/products/expert_assessment/season_drought.png
[27] P.C.D. Milly and K.A. Dunne. “Colorado River flow dwindles as warming-driven loss of reflective snow energizes evaporation”, Science, 367 (6483) , (2020): 1252-1255. DOI: 10.1126/science.aay9187
[28] M. Reisner. Cadillac Desert: The American West and its Disappearing Water, Revised and Updated. (New York: Penguin Books, 1993).
[29] P. Fradkin. A river no more: The Colorado River and the west. (Los Angeles:University of California Press, 1996).
[30] Y. Chikamoto et al. “Colorado River water supply is predictable on multi-year timescales owing to long-term ocean memory”, Nature Communications: Earth and Environment, 1, 26(2020). https://doi.org/10.1038/s43247-020-00027-0
[31]Ghosh and Bandyopadhyay. “A Scarcity Value based Explanation of Trans-boundary Water Disputes”.
[32]Ghosh. Economics of Hostile Hydropolitics over Transboundary Waters: Scarcity Values and Interstate Water Conflicts in India and US.
[33] Ghosh and Bandyopadhyay. “A Scarcity Value based Explanation of Trans-boundary Water Disputes”.
The views expressed above belong to the author(s). ORF research and analyses now available on Telegram! Click here to access our curated content — blogs, longforms and interviews.

 PDF Download
PDF Download





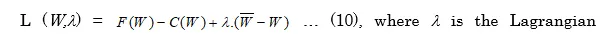


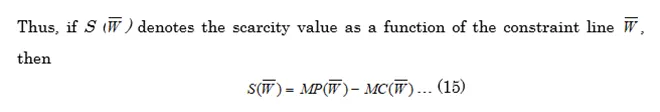






 PREV
PREV


